如何对待DeepMind最新的AI系统AlphaTensor可以发现矩阵相乘的求解方式？

我是boy知道吗 · 发表于 2023-6-28 09:43:15

Nature最新一篇文章：Discovering faster matrix multiplication algorithms with reinforcement learning | Nature

lixiaoyiwenku · 发表于 2023-6-28 09:43:21

前言
这篇文章的主要内容是，解读 AlphaTensor 这篇论文的主要思想，如何通过强化学习来探索发现更高效的矩阵乘算法。
1、二进制加法和乘法

这一节简单介绍一下计算机是怎么实现加法和乘法的。
以 2 + 5 和 2 * 5 为例。
我们知道数字在计算机中是以二进制形式表示的。
整数2的二进制表示为： 0010
整数5的二进制表示为： 0101
1.1、二进制加法

二进制加法很简单，也就是两个二进制数按位相加，如下图所示：

当然具体到硬件实现其实是包含了异或运算和与运算，具体细节可以阅读文末参考的资料。
1.2、二进制乘法

二进制乘法其实也是通过二进制加法来实现的，如下图所示：

乘法在硬件上的实现本质是移位相加。
对于二进制数来说乘数和被乘数的每一位非0即1。
所以相当于乘数中的每一位从低位到高位，分别和被乘数的每一位进行与运算并产生其相应的局部乘积，再将这些局部乘积左移一位与上次的和相加。
从乘数的最低位开始：
若为1，则复制被乘数，并左移一位与上一次的和相加;
若为0，则直接将0左移一位与上一次的和相加；
如此循环至乘数的最高位。
从二进制乘法的实现也可以看出来，加法比乘法操作要快。
1.3、用加法替换乘法的简单例子

上面这个公式相信大家都很熟悉了，式子两边是等价的
左边包含了2次乘法和1次加法（减法也可以看成加法）
右边则包含了1次乘法和2次加法
可以看到通过数学上的等价变换，增加了加法的次数同时减少了乘法的次数。
2、矩阵乘算法

对于两个大小分别为 Q x R 和 R x P 的矩阵相乘，通用的实现就需要 Q * P * R 次乘法操作（输出矩阵大小 Q x P，总共 Q * P 个元素，每个元素计算需要 R 次乘法操作）。
根据前面 1.2内容可知，乘法比加法慢，所以如果能减少的乘法次数就能有效加速矩阵乘的运算。
2.1、通用矩阵乘算法

首先来看一下通用的矩阵乘算法:

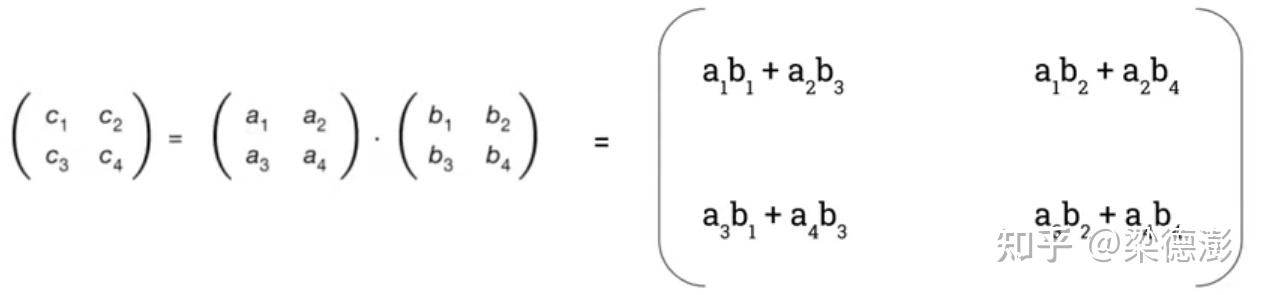
如上图所示，两个大小为2x2矩阵做乘法，总共需要8次乘法和4次加法。
2.2、Strassen 矩阵乘算法

上图所示即为 Strassen 矩阵乘算法，和通用矩阵乘算法不一样的地方是，引入了7个中间变量 m，只有在计算这7个中间变量才会用到乘法。
简单用 c1 验证一下：

可以看到 Strassen 算法总共包含7次乘法和18次加法，通过数学上的等价变换减少了1次乘法同时增加了14次加法。
3、AlphaTensor 核心思想解读

3.1、将矩阵乘表示为3维张量

首先来看下论文中的一张图

图中下方是3维张量，每个立方体表示3维张量一个坐标点。
其中张量每个位置的值只能是 0 或者 1，透明的立方体表示 0，紫色的立方体表示 1。
现在将图简化一下，以[a,b,c]这样的维度顺序，将张量以维度a平摊开，这样更容易理解：

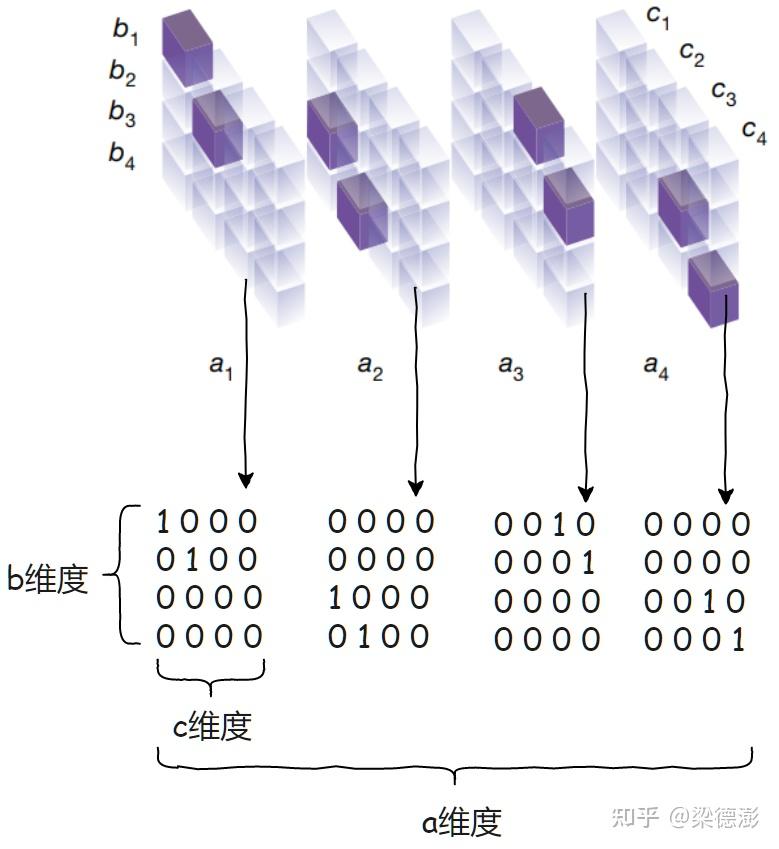
这个3维张量怎么理解呢？
比如对于 c1，我们知道 c1 的计算需要用到 a1,a2,b1,b3，对应到3维张量就是：

而从上图可知，对于两个 2 x 2 的矩阵相乘，3维张量大小为 4 x 4 x 4。
一般的，对于两个 n x n 的矩阵相乘，3维张量大小为 n^2 x n^2 x n^2。
更一般的，对于两个 n x m 和 m x p 的矩阵相乘，3维张量大小为 n*m x m*p x n*p。
然后论文中为了简化理解，都是以 n x n 矩阵乘来讲解的，论文中以

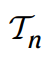
表示 n x n 矩阵乘的3维张量，下文中为了方便写作以 Tn 来表示。
3.2、3维张量分解

然后论文中提出了一个假设：
如果能将3维张量 Tn 分解为 R 个秩1的3维张量（R rank-one terms）的和的话，那么对于任意的 n x n 矩阵乘计算就只需要 R 次乘法。

如上图公式所示，就是表示的这个分解，其中的

就表示的一个秩1的3维张量，是由 u^(r) 、 v^(r) 和 w^(r) 这3个一维向量做外积得到的。
这具体怎么什么理解呢？我们回去看一下 Strassen 矩阵乘算法：

上图左边就是 Strassen 矩阵乘算法的计算过程，右边的 U，V 和 W 3个矩阵，各自分别对应左边 U -> a， V -> b 和 W -> m。
具体又怎么理解这三个矩阵呢？

我们在图上加一些标注来解释，其中 U ， V 和 W 矩阵每一列从左到右按顺序，就对应上文提到的，u^(r) 、 v^(r) 和 w^(r) 这3个一维向量。
然后矩阵 U 每一列和 [a1,a2,a3,a4] 做内积，矩阵 V 每一列和 [b1,b2,b3,b4] 做内积，然后内积结果相乘就得到 [m1,m2,m3,m4,m5,m6,m7]了。
最后矩阵 W 每一行和 [m1,m2,m3,m4,m5,m6,m7] 做内积就得到 [c1,c2,c3,c4]。
接着再看一下的 U，V 和 W 这三个矩阵第一列的外积结果

如下图所示：

可以看到 U，V 和 W 三个矩阵每一列对应的外积的结果就是一个3维张量，那么这些3维张量全部加起来就会得到 Tn 么？下面我们来验证一下：

可以看到这些外积的结果全部加起来就恰好等于 Tn：

所以也就证实了开头的假设:
如果能将表示矩阵乘的3维张量 Tn 分解为 R 个秩1的3维张量（R rank-one terms）的和，那么对于任意的 n x n 矩阵乘计算就只需要 R 次乘法。

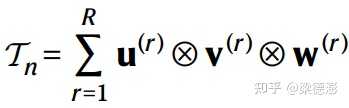
因此也就很自然的可以想到，如果能找到更优的张量分解，也就是让 R 更小的话，那么就相当于找到乘法次数更小的矩阵乘算法了。
通过强化学习探索更优的3维张量分解

将探索3维张量分解过程变成游戏

论文中是采用了强化学习这个框架，来探索对3维张量Tn的更优的分解。强化学习的环境是一个单玩家的游戏（a single-player game, TensorGame）。
首先定义这个游戏进行 t 步之后的状态为 St：

然后初始状态 S0 就设置为要分解的3维张量 Tn：

对于游戏中的每一步t，玩家（就是本论文提出的 AlphaTensor）会根据当前的状态选择下一步的行动，也就是通过生成新的三个一维向量从而得到新的秩1张量：

接着更新状态 St减去这个秩1张量：

玩家的目标就是，让最终状态 St=0同时尽量的减少游戏的步数。
当到达最终状态 St=0 之后，也就找到了3维张量Tn的一个分解了：

还有些细节是，对于玩家每一步的选择都是给一个 -1 的分数奖励，其实也很容易理解，也就是玩的步数越多，奖励越低，从而鼓励玩家用更少的步数完成游戏。
而且对于一维向量的生成，也做了限制

就是生成这些一维向量的值，只限定在比如 [−2, −1, 0, 1, 2] 这5个离散值之内。
AlphaTensor 简要解读

论文中是怎么说的，在游戏过程中玩家 AlphaTensor 是通过一个深度神经网络来指导蒙特卡洛树搜索（MonteCarlo tree search）。关于这个蒙特卡洛树搜索，我不是很了解这里就不做解读了，有兴趣的读者可以阅读文末参考资料。
首先看下深渡神经网络部分：

深度神经网络的输入是当前的状态 St也就是需要分解的张量（上图中的最右边的粉红色立方体）。输出包含两个部分，分别是 Policy head 和 Value head。
其中 Policy head 的输出是对于当前状态可以采取的潜在下一步行动，也就是一维向量(u(t), v(t), w(t)) 的候选分布，然后通过采样得到下一步的行动。
然后 Value head 应该是对于给定的当前的状态 St ，估计游戏完成之后的最终奖励分数的分布。
接下来简要解读一下整个游戏的流程，还有深度神经网络是如何训练的：

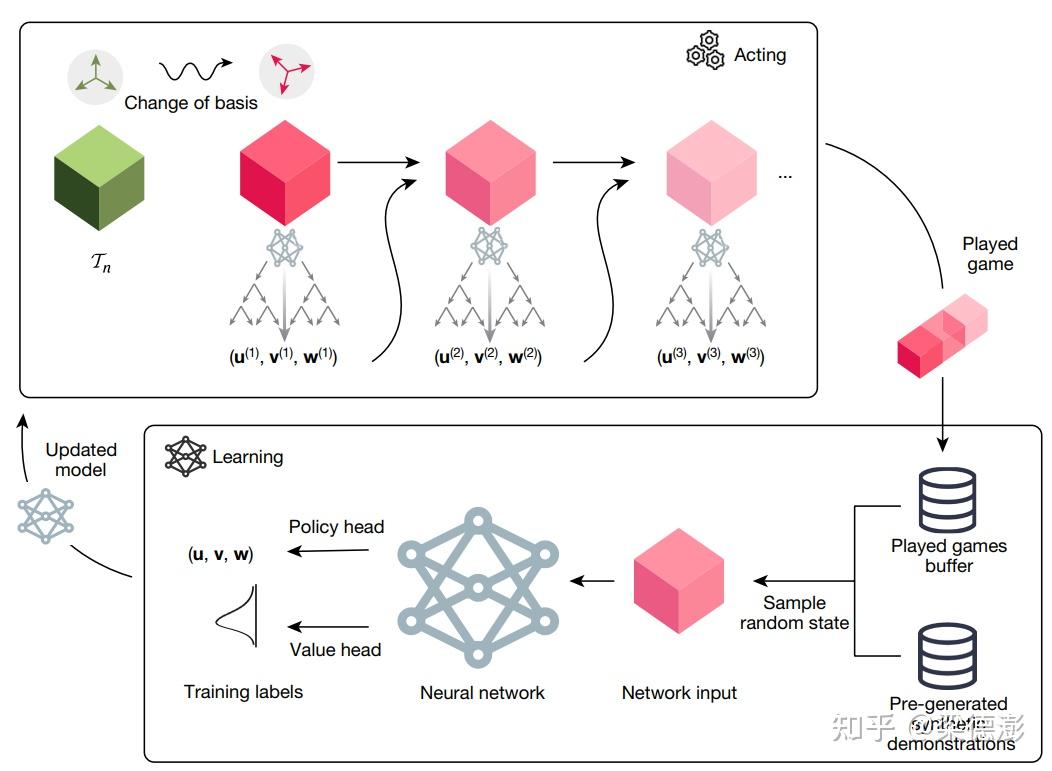
先看流程图的上方 Acting 那个方框内，表示的是用训练好的网络做推理玩游戏的过程。
可以看到最左边绿色的立方体，也就是待分解的3维张量 Tn变换到粉红色立方体，论文中提到是作了基的变换，但是这块感觉如果不是去复现就不用了解的那么深入，而且我也没去细看这块就跳过吧。
然后从最初待分解的 Tn 开始，输入到神经网络，通过蒙特卡洛树搜索得到秩1张量，然后减去该张量之后，继续将相减的结果输入到网路中，继续这个过程直到张量相减的结果为0。
将游戏过程记录下来，就是流程图最右边的 Played game。
然后流程图下方的 Learning 方框表示的就是训练过程，训练数据有两个部分，一个是已经玩过的游戏记录 Played games buffer 还有就是通过人工生成的数据。
人工怎么生成训练数据呢？
论文中提到，尽管张量分解是个 NP-hard 的问题，给定一个 Tn 要找其分解很难。但是我们可以反过来用秩1张量来构造出一个待分解的张量嘛！简单来说就是采样R个秩1张量，然后加起来就能的到分解的张量了。
因为对于强化学习这块我不是了解的并不深入，所以也就只能作粗浅的解读。
实验结果

最后看一下实验结果

表格最左边一列表示矩阵乘的规模，最右边三列表示矩阵乘算法乘法次数。
第一列表示目前为止，数学家找到的最优乘法次数。
第2和3列就是 AlphaTensor 找到的最优乘法次数。
可以看到其中有5个规模，AlphaTensor 能找到更优的乘法次数（标红的部分）：
两个 4 x 4 和 4 x 4 的矩阵乘，AlphaTensor 搜索出47次乘法；
两个 5 x 5 和 5 x 5 的矩阵乘，AlphaTensor 搜索出96次乘法；
两个 3 x 4 和 4 x 5 的矩阵乘，AlphaTensor 搜索出47次乘法；
两个 4 x 4 和 4 x 5 的矩阵乘，AlphaTensor 搜索出63次乘法；
两个 4 x 5 和 5 x 5 的矩阵乘，AlphaTensor 搜索出76次乘法；
参考资料

Discovering faster matrix multiplication algorithms with reinforcement learning - Nature This is a game changer! (AlphaTensor by DeepMind explained)AlphaTensor by DeepMind Explained – Talk by Emma Chen at Harvard Medical AI Lab Hardware for addition and subtraction: By OpenStax (Page 3/3)「一沙一世界」之硬件加法器-面包板社区硬件乘法器_百度百科 [算法系列之十五]Strassen矩阵相乘算法_@SmartSi的博客-CSDN博客 AlphaZero Explained What is Monte Carlo Tree Search? - Artificial Intelligence Alpha Zero and Monte Carlo Tree Search 蒙特卡洛树搜索｜AlphaGo的核心算法

麦斯威尔咖啡 · 发表于 2023-6-28 09:44:15

先说结论：DeepMind的这篇文章，是探索更复杂Strassen的工作，有理论意义。至于实际的工程意义，是否真的能加速科学计算，要打一个大的问号。
矩阵相乘的Strassen算法

一个2x2的矩阵乘法，原来需要8次乘法计算，采用了Strassen算法计算的次数只需要7次 (m1 -- m7的计算部分)

Strassen算法最早在[1]中就提出，可以减少矩阵乘法计算中的乘法次数。对应的，加法次数会有一点增加。通过递归的方法，2x2的Strassen矩阵乘法，可以扩展到4x4乃至更大矩阵。
为什么关注乘法次数，不关注加法次数？

最简单的64位整数的乘法计算 [2]：需要一个64位的加法器，进行64次的加法计算。

从简单的乘法器可以看出，乘法计算其实可以拆解成很多的加法计算（64位整数的乘法需要进行64次的加法计算）。所以一般计算中，我们可以只关注乘法带来的开销。
关注乘法次数就够了吗？

不够的。
矩阵乘法在很多科学计算领域，都有着广泛的应用（举一个例子，深度学习DNN的计算过程，可以拆解成一系列的矩阵计算）。IJCNN&#39;14 [3] 的工作，就利用Strassen算法加速了DNN inference。学术界在接下来并没有更多的探索Strassen加速DNN。终极原因：Strassen不够快。
在CPU/GPU上面进行矩阵计算，要关注计算，和数据传输 两个维度。下图的Roofline模型是很通用的估计系统性能模型。一个好的计算模型，需要同时在计算和数据传输上获得高效率。

Roofline模型：横坐标是计算密度，纵坐标是数据传输效率。峰值性能 (peak performance) 需要计算能力和数据传输能力都满足的情况

计算，顾名思义，就是计算量尽量小，避免重复计算。Strassen算法以及这篇Nature工作，是一个很好的例子。
数据传输，回忆一下本科时候学的计算机组成原理课程，我们的CPU/GPU里面采用了层次式的存储器结构（Register file-->Cache-->Main memory-->SSD/hard disck），以达到性能价格速度的一个平衡。为了充分利用存储结构，我们需要我们的算法满足 spatial locality & temporal locality。

Spatial locality: 当我们访问了一个数，我们最好接着访问这个数的邻居
Temporal locality: 当我们从cache中加入一个数，充分访问它。它被挪出Cache后就别再访问

例子1:
for(int i=0; i<1024; i++){
      for(int j=0; j<1024; j++){
         sum += a_arr[j] * b_arr[j];
      }
}
例子2：
for(int i=0; i<1024; i++){
      for(int j=0; j<1024; j++){
         sum += a_arr[j] * b_arr[j];
      }
}
以上两个例子，都是做矩阵点乘，功能完全一样，计算复杂度完全一样。但就因为数据访问的不同，运行时间有10倍的差距（实测过）。
Strassen只修炼终极乘法次数，没有修炼数据访存友好，偏科了。Nature这篇的实验结果，也只是跟Strassen进行了比较。
怎样搜索一个真正快速的矩阵乘法？

这个是一个非常大的话题，作为这么古老的题目，一直到现在还有很多博士生和研究人员，孜孜不倦的进行着探索。用到的方法有好多种，例如：考虑两个矩阵的数据访问排列（for loop顺序）；tiling （把大的矩阵进行拆分）；loop unrolling (把矩阵的一些部分做降维)。这些因素都考虑进去，矩阵乘法是一个维度特别大的搜索空间。
下面课件对卷积计算加速方法进行了简单讨论：
CUHK CMSC5743-卷积计算加速
[1] Strassen, Volker. &#34;Gaussian elimination is not optimal.&#34;Numerische mathematik13.4 (1969): 354-356.
[2] Patterson, David A., and John L. Hennessy.Computer organization and design ARM edition: the hardware software interface. Morgan kaufmann, 2016.
[3] Cong, Jason, and Bingjun Xiao. &#34;Minimizing computation in convolutional neural networks.&#34;International conference on artificial neural networks. Springer, Cham, 2014.

xinbohefang · 发表于 2023-6-28 09:44:21

谢谢我们学生的邀请。。。
论文概括来说，是针对矩阵乘法过程定义了特别的搜索空间并在随机样例上用高度剪枝的搜索算法(AlphaZero)搜出答案。AlphaZero方法本身的创新性不多，接下来再仔细看一眼文章里的related work，以及几篇missing references：
B. Andreatto, A. Cariow. Automatic generation of fast algorithms for matrix–vector multiplication. International Journal of Computer Mathematics, 2018.
Jianyu Huang, Leslie Rice, Devin A. Matthews, Robert A. van de Geijn. Generating Families of Practical Fast Matrix Multiplication Algorithms. In: Proceedings of 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS 2017).
Marijn J.H. Heule, Manuel Kauers, Martina Seidl. Local Search for Fast Matrix Multiplication. In: Proceedings of the 22nd International Conference on Theory and Applications of Satisfiability Testing (SAT 2019), LNCS 11628: 155-163.
就可以看到，对于搜索算法的tensor表征等都已是前人的成果，前人已经做到了用不同的搜索算法来搜，搜出几千个等价的之类的成果之前也已做到，即图1和算法1都不是本文的贡献，本文既不是开创者也不是终结者。本文的贡献在于用AlphaZero来搜。最大的价值可能在于针对硬件特性的优化一节。
我比较好奇的是，本文强调了一个新的发现，即4x4直接搜比退化为2x2的递归要快，也就是说递归本身不是最优的，指出了需要随着问题规模nxn的增长进行直接的分解。然而本文学习的模型在问题规模上没有泛化能力，是完全当作优化器在用。这似乎也强调了本文方法的局限。
由于训练任务是自己生成的，也就知道了每一步是怎么走的，因此本文使用了监督学习loss+RL loss，然而缺少ablation study分析两个loss的作用。
另外，对于本文提到的(3,3,3)问题最优解未知，本文的搜索也没有给出更好的回答。

麥葬諾言 · 发表于 2023-6-28 09:45:17

谢邀请（系统自动邀请的么？）
先说结论：从高性能计算的角度, 快速矩阵乘算法已经实用了，AlphaTensor的结果离落地还有距离。
第一，大型稠密矩阵乘一直被认为是计算受限的，浮点计算次数决定程序运行的时间。AlphaTensor的结果针对的是计算次数，首先现在的处理器一般会支持乘加融合指令，也就是说c=c+a*b只算一条指令，所以减少乘法增加加法未必能真的减少浮点计算指令的数目，也就不一定有加速效果。再者矩阵乘的计算访存比~100，如果浮点计算次数下降到一个程度，矩阵乘会变成访存受限，这样快速矩阵乘也就没有实用意义了。
第二，AlphaTensor也没有考虑数值稳定性，快速矩阵乘法的数值稳定性一般都比普通的 $O(N^{3})$ 分块算法差，而数值不稳定的算法实用性存疑。
第三，对于实际处理器而言，矩阵乘实现还需要向量化或者适合矩阵加速部件（比如Systolic Arrays，Tensor Core）。快速矩阵乘的表达式如果太散，由于片上存储能放下的矩阵元素有限，可能会出现难以利用向量或者矩阵计算部件的问题。
关于快速矩阵乘算法库研究（可以落地的），我印象最深的是BLIS组Robert A. van de Geijn在2016年完成的高性能Strassen矩阵乘。总体结论如下

多层的Strassen算法

层数一多就难以保证数值稳定性。性能方面，定义有效性能 $2n^{3}/t$ ，因为实际上快速矩阵乘法的浮点计算次数不是 $2n^{3}$ ，这里方便比较定义了有效性能。多核CPU的结果为

还是能够在实际的CPU上有效果的。在GPU Tesla V100 SXM2 accelerator上，结果为

Tesla V100 SXM2 accelerator

方法还是寄存器重用，汇编那一套。至少说明一部分数值稳定的快速矩阵乘法确实是能落地的，但是AlphaTensor的结果仅仅只是理论上的，离工业上落地还有一段距离，得看看能不能从AlphaTensor做出来的结果里面找到一些可实用的快速矩阵乘算法。（估计很难）
另一方面不得不说，AlphaTensor的方法是很有意思的，或许可以为复杂的计算的算子融合提供解决思路。

小博园 · 发表于 2023-6-28 09:45:48

这学期在做研究生课程《矩阵分析与应用》的助教，AlphaTensor正好是一个和矩阵应用非常相关的工作，这里我就简单来分析一下DeepMind这篇工作究竟在干什么。学过克罗内克积、低秩分解、强化学习的同学就可以看懂我的这篇回答。
这篇回答仅作为一个不严谨的文章简介，希望各位看官轻喷。
快速矩阵乘法问题

矩阵乘法是一个具有广泛应用的基础操作，提高这种基础运算的计算效率会带来广泛的应用。标准的矩阵乘法是由数值的加法和乘法组成的。我们知道，在计算机中，乘法带来的计算消耗远大于加法带来的计算消耗。快速矩阵乘法问题就是去寻找数值乘法次数更少的矩阵乘法算法的问题。
长期以来，人们认为标准的矩阵乘法算法就是最优的算法。然而，1969年，德国数学家Volken Strassen在 $2\times2$ 矩阵上发现了一种更为快速的算法打破了人们的这一观点：

2×2矩阵上的标准矩阵乘法和Strassen算法

由此，人们开始用各种方法解决快速矩阵乘法问题。然而，直到现在，我们甚至不能找到在 $3\times3$ 上的最快速的矩阵乘法算法。（我们可以直观理解一下这个问题的难度：上图的Strassen算法中，我们只是对矩阵不同元素使用了系数为1的加减法。如果系数不为1，而是所有自然数、甚至有理数，那么这样的算法搜索空间将会非常巨大。）
将快速矩阵乘法问题转化为低秩张量分解问题

（为了能够使用RL，）科学家们将上述的快速矩阵乘法问题转化为了低秩张量分解问题。这里分为两步：

用张量表示矩阵乘法

我们用一个 $\times$ $\times n^2$ 的表示张量来表示两个矩阵相乘的过程（ $A_{n\times n}B_{n\times n}=C_{n\times n}$ ）。如下图所示，我们取 $n=2$ 来举例。表示张量的三个维度分别表示三个矩阵的元素（在下图中，从左到右的维度是 $a$ ，从上到下的维度是 $b$ ，从前到后的维度是 $c$ ）。我们用 $\{0,1\}$ 填充这个表示张量，其中矩阵 $C$ 取值的地方染色为，其余地方染色为。（例如下图中， $c_1=a_1b_1+a_2b_3$ ，那么 $c_1$ 对应的最后面一层的最左上角的方块、第三排第二列的方块就被染成了紫色，即变成。）

2×2矩阵乘法的表示张量

值得注意的是，表示张量只和矩阵的形状有关，而和矩阵的值无关。
2. 张量的低秩分解和矩阵乘法的对应算法
我们首先回顾一下矩阵的低秩分解：对于一个 $m\times n$ 的矩阵  ，我们想把它分解为形状分别是 $m\times r$ 和 $r\times n$ 的两个矩阵相乘，即 $A_{m\times n}=U_{m\times r}V_{r\times n}$ 。
值得一提的是，上式从右到左的计算除了用标准的矩阵乘法将两个矩阵相乘，还可以这样计算：设的  每一列向量为  ，  的每一行向量为 $V_i^T$ ， $i=1,\cdots,r$ 。那么我们可以将  表示为  个矩阵的和：
$A_{m\times n}=\sum_{i=1}^{r}U_iV_i^T$
回到原问题，表示张量的低秩分解问题是：设  为两个  矩阵相乘的表示张量，我们将分解为个秩一项(rank-one term)的外积（一种特殊的克罗内克积）：
$T_n=\sum_{i=1}^{r}U_i\otimes V_i\otimes W_i$
其中  ，  ，  均为  维向量。两个维向量的外积可以得到一个的矩阵，三个维向量的外积可以得到一个 $n\times n \times n$ 的张量（参考，学过矩阵的同学可以想象为一种克罗内克积）。
那么表示张量的低秩分解和原问题有什么关系呢？请看下图：

2×2的Strassen算法和其表示张量的秩7分解

上面（b）是 $2\times 2$ 矩阵乘法的Strassen算法，（c）是 $4\times 4 \times 4$ 的表示张量的秩7分解结果，其中的，  ， $W$ 的每一列就是表示张量低秩分解算法中的，  ，  。我们可以发现由（c）可以设计一种规则，一一对应地得到图（b）的矩阵乘法算法，这正是论文中的算法1：

张量低秩分解的结果导出的矩阵乘法算法

再根据参考文献[1]，张量分解的秩越小，这样导出的矩阵乘法算法中的乘法次数越少。因此，我们成功地将“寻找快速矩阵乘法算法”的问题，转化为“寻找张量表示的低秩分解”问题。
值得一提的是，在AlphaTensor之前，人们已经明白了这个转化过程，并已经使用各种搜索算法来求解这个问题了。AlphaTensor的主要贡献是将搜索算法换为深度强化学习并取得了很棒的结果。
将低秩张量分解问题建模为强化学习问题

那么如何对任意矩阵乘法的表示张量进行低秩分解呢？AlphaTensor将这个过程设计了一个强化学习问题，简单来说是这样子的：
设环境的初始状态 $S_0=T_n$ （输入待分解的表示张量），agent在每一步都输出三个向量 $\{U_t$ ， $V_t$ ， $W_t\}$ ，环境状态转化为 $S_t=S_{t-1}-U_t\otimes V_t\otimes W_t$ ，agent获得单步奖励-1，环境在 $S_t=0$ 或者达到设置的最大步数 $T_{limit}$ 时停止，若达到最大步数时剩余张量不为  ，则获得一个终点奖励 $-R_{limit}$ ，其绝对值为张量 $S_{T_{limit}}$ 的秩。
从这个过程我们可以看出，AlphaTensor不断减去每一步输出的矩阵从而训练这个agent以最快的步数把表示张量减到0（每一步的负奖励）。这个最快的步数就是最后得到的分解的秩。
使用Transformer和MCTS来训练

建模为强化学习之后就可以训练啦。AlphaTensor使用了和AlphaZero相似的MCTS方法来训练这个RL agent。AlphaTensor使用了Transformer作为backbone（并魔改了self-attention为axial-attention）。网络每一步除了输出向量，还要估计当前的value（相当于当前的张量秩）。
AlphaTensor使用人造数据（sample一些分解结果然后把他们乘起来）来训练这个网络，并且还有一些其他trick（change of basis等，这一部分的详细过程请参见原文。）整个过程如图所示。

AlphaTensor的训练过程

网络在小于等于5维的矩阵相乘上做了细粒度的实验，还在最多12维的矩阵上做了分块矩阵的实验（由此可以看出我们离大规模矩阵快速乘法算法还有很遥远的距离...）。从结果来看，AlphaTensor可以取得和之前人工算法相同或者更优秀的结果。
值得注意的是，对于每一种形状的矩阵相乘，AlphaTensor可以获得数千个互相不等价的最优算法（也就是说本来可以一下子发几千个paper嘿嘿）。未来的研究者可以从这些搜索到的算法中学习一下他们的pattern，来启发更好的矩阵乘法算法（就像是现在围棋选手学习AlphaGo）。

AlphaTensor的实验结果

总结

AlphaTensor真的是一项非常棒的工作。可惜DeepMind没有放出网络结构的源码（不如设置为矩阵大作业吧）。

		自动登录	找回密码
密码			立即注册

如何对待DeepMind最新的AI系统AlphaTensor可以发现矩阵相乘的求解方式？

本帖子中包含更多资源

本帖子中包含更多资源

本帖子中包含更多资源

本帖子中包含更多资源